
트리(Tree)
Tree는 서로 연결된 Node의 계층형 자료구조로써, root와 부모-자식 관계의 subtree로 구성되어 있습니다. 리스트가 단순히 순서를 매겨 데이터를 나열하는 선형 자료구조라면, 트리는 비선형적인 자료구조입니다.⁽¹⁾
트리는 root에서 시작하여 여러 개의 tree가 중첩되는 형태로 만들어집니다. 그렇기에 하나의 tree안에 여러 개의 subtree가 존재합니다.

Tree 관련 개념
기본적인 트리 관련 용어를 정리해 보도록 하겠습니다.
- 정점 (Vertex): A,B,C와 같은 값을 갖고 나타내며, 노드로 표현됩니다.
- 간선 (Edge): 정점 간에 연결된 선입니다.
- 자식 노드 (Child), 부모 노드 (Parent)
- 형제 노드(Sibling): 같은 부모를 가진 노드를 말합니다.
- 리프 노드 (Leef): 더 이상 뻗어나갈 수 없는 마지막 노드를 일컫습니다.

- 차수 (degree): 각 노드가 갖는 자식의 수. 모든 노드의 차수가 n개 이하인 트리를 n진 트리라고 합니다.

- 조상 (ancestor) 위쪽으로 간선을 따라가면 만나는 노드들 말합니다.
- 자손 (descendant): 아래쪽으로 간선을 따라가면 만나는 노드들을 말합니다.
- 루트 노드(Root): 트리의 시작 점입니다.
- 높이 (height): 루트 노드에서 가장 멀리 있는 리프 노드까지의 거리입니다.
- 레벨 (level): 루트 노드에서 떨어진 거리입니다.

트리 순회
선형 자료구조인 배열과 리스트의 경우, 순회하는 법이 인덱스 0,1,2부터 n-1까지로 방법이 하나로 정해져 있기 때문에, 순회하는 방법을 따로 배우지 않았습니다. for문을 이용해서 쉽게 순회할 수 있기 때문이죠. 하지만 트리는 비선형 자료구조이기에 순회하는 방법이 여러가지 존재합니다. 대표적인 방법들로 level order traversal, preorder traversal, inorder traversal, postorder traversal이 있습니다.
순회에 대해 설명을 하기 전에 방문(visit)한다는 것과 순회(traversal)한다는 것에 대한 용어 정의가 필요합니다.
비슷하지만 약간의 뉘앙스가 다릅니다. 트리에서의 순회는 트리를 돌아다니는 것이고, 트리에서의 방문은 노드의 값에 접근하는 것(출력, 저장 등의 행위)입니다.
Level-order traversal
저희는 앞서서 level에 대해 정의 해보았습니다. level은 root 노드에서 떨어진 거리를 말합니다.

다음과 같이 root가 A인 tree가 있다고 합시다.

level order traversal은 말 그대로 level 별로 순회하는 것을 말합니다.
(A) →(B, C, D) → (E, F, G, H, I) → (J, K, L)
level order traversal 구현
level order traversal의 탐색 방법을 알았으니, 코드를 구현해 볼 차례입니다.
💡 level order의 구현 코드는 아주 기본적인 템플릿으로, 다음부터는 코드를 참고하지 않고도 직접 짤 수 있어야 합니다‼️
from collections import deque
def levelOrder(root):
visited = []
if root is None:
return 0
q = deque()
q.append(root)
while q:
cur_node = q.popleft()
visited.append(cur_node.value)
if cur_node.left:
q.append(cur_node.left)
if cur_node.right:
q.append(cur_node.right)
return visited
queue를 사용함으로써, level order traversal를 구현해 보았습니다. queue를 popleft하고 append함으로써 각 노드를 방문하는 과정과 queue가 비게 되면, 완전 탐색이 끝난다는 것이 핵심입니다.
코딩 테스트에서는 위 과정들이 머릿속에서 그려지고, 코드들을 바로바로 짤 수 있어야 합니다.
Level order traversal 시간 복잡도
levelOrder의 시간복잡도는 어려울 게 없습니다. 모든 정점의 개수가 n에 대해, popleft하고 append하는 과정이 n번 일어나므로 $O(n)$의 시간복잡도를 가집니다. 총 $n$개의 node를 탐방해야하므로 $O(n)$의 시간복잡도를 가진다고 생각해도 좋습니다.
전위순회, 중위순회, 후위순회
**전위 순회(preorder), 중위 순회(inorder), 후위 순회(postorder)**의 구현은 앞서 배운 level order traversal에 비해 상대적으로 쉽습니다.
우선 순회하는 것을 먼저 보도록 하겠습니다.

모든 트리는 기본적으로 다음과 같이 생겼습니다. 재귀적으로 정의 되어 있기 때문에 한 세트에서의 순회 과정을 정의하면 전체 트리를 순회할 수 있습니다.

시작 노드에서 왼쪽 자식 노드, 다시 시작 노드를 거친 후 오른쪽 자식 노드를 찍고 마지막으로 시작 노드를 가는 것이 트리 순회의 과정입니다.
A→B→A→C→A
다른 예를 봐보도록 합시다.

어떤 식으로 순회할 수 있는지 한 번 생각 해보세요!

def traversal(root):
if root is None:
return
traversal(root.left)
traversal(root.right)
위와 같은 코드에서 언제 방문할지에 따라 전위, 중위, 후위의 코드가 결정됩니다.
각각의 코드를 구현해보도록 합시다.
전위 순회 구현
def preorder(root):
if root is None:
return
print(root.value)
preorder(root.left)
preorder(root.right)
중위 순회 구현
def inorder(root):
if root is None:
return
inorder(root.left)
print(root.value)
inorder(root.right)
후위 순회 구현
def postorder(root):
if root is None:
return
postorder(root.left)
postorder(root.right)
print(root.value)
전위, 중위, 후위 순회 시간복잡도
💡 재귀의 시간복잡도 = 재귀 함수 호출 수 x (재귀 함수 하나당) 시간복잡도
저희는 앞서서 재귀의 시간복잡도를 위와 같이 공부하였습니다. 전위, 중위, 후위 순회의 시간 복잡도도 마찬가지로 구할 수 있습니다.
- 재귀 함수 호출 수 : $n$
- 재귀 함수 하나당 시간 복잡도: $O(1)$
⇒ 전위, 중위, 후위 순회의 시간 복잡도는 $O(n)$입니다.
코딩테스트 활용
코딩테스트에서 트리 문제를 해결하기 위해서는, 별다른 팁이 존재한다기보다, 기본적인 트리의 구조를 잘 알고 있어야 합니다. 트리 자료구조를 활용하는 문제보다 트리의 개념을 활용한 문제가 주로 나오기 때문이죠.
대표적인 예시로 백준의 후위 표기식 문제가 있습니다. 해당 문제는 중위 표기식을 후위 표기식으로 변환하는 문제로 트리의 순회 방법인 중위, 후위 순회의 개념이 사용되었지만, 실제로 푸는 방식은 스택 자료구조를 사용하여 해결하는 것이 대표적입니다. 이와 같이 트리의 개념과 추가로 전위 순회, 중위 순회, 후위 순회, 이 3가지 방식에 대해서도 이해하고 코드로 구현할 줄 아신다면, 트리를 활용한 문제를 잘 해결할 수 있을 것입니다.
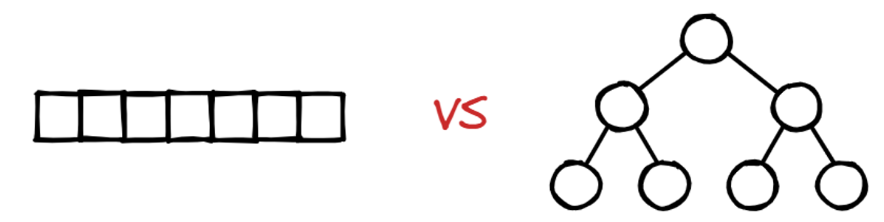
**1. 선형 자료구조 vs 비선형 자료구조**
- 선형 자료구조 : 하나의 자료 뒤에 하나의 자료가 존재하는 것
- 비선형 자료구조 : 하나의 자료 뒤에 여러개의 자료가 존재하는 것
'코딩테스트 [킬링캠프]' 카테고리의 다른 글
| 2.8 그래프 (Graph, Dijkstra) (0) | 2024.01.03 |
|---|---|
| 2.7 힙 (Heap - Priority queue) (2) | 2024.01.03 |
| 2.5 이진 탐색 (Binary Search) (1) | 2024.01.03 |
| 2.4 재귀 (Recursion) (1) | 2024.01.03 |
| 2.3 해시테이블 (Hash Table) (1) | 2024.01.03 |
